L’articolo è stato aggiunto alla lista dei desideri
LIBRO
E-mail
Facebook
LinkedIn
Twitter
WhatsApp
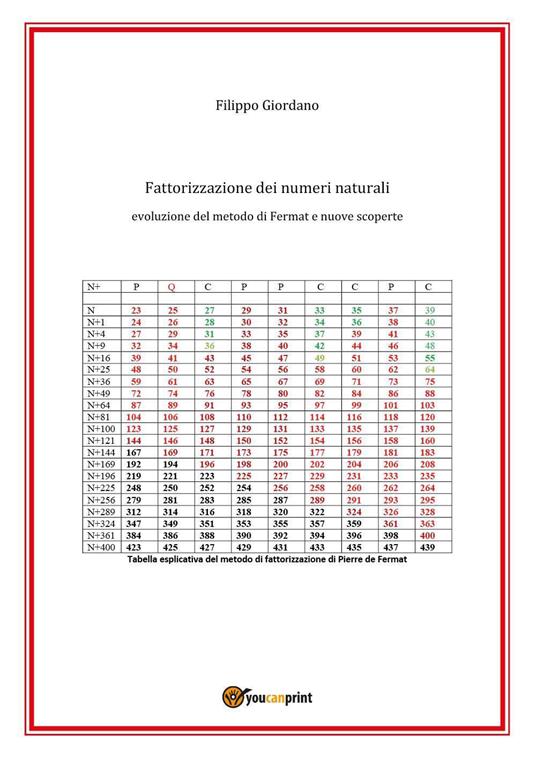
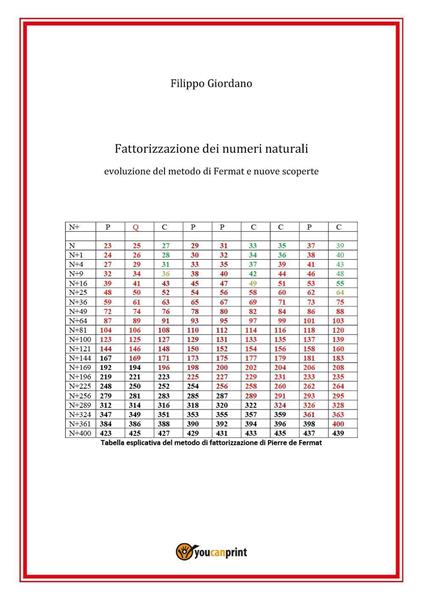
Fattorizzazione dei numeri naturali. Evoluzione del metodo di Fermat e nuove scoperte
(0)
Cliccando su “Conferma” dichiari che il contenuto da te inserito è conforme alle Condizioni Generali d’Uso del Sito ed alle Linee Guida sui Contenuti Vietati. Puoi rileggere e modificare e successivamente confermare il tuo contenuto. Tra poche ore lo troverai online (in caso contrario verifica la conformità del contenuto alle policy del Sito).
Grazie per la tua recensione!
Tra poche ore la vedrai online (in caso contrario verifica la conformità del testo alle nostre linee guida). Dopo la pubblicazione per te +4 punti 
11,88 €
-5%
12,50 €
+120
punti
Venditore: IBS
(Altre 1 offerte da 11,88 €)
Articolo acquistabile con Carta del Docente
Articolo acquistabile con Carta Cultura Giovani e Carta del Merito
Dati e Statistiche
Salvato in 0 liste dei desideri
Salvato in 0 liste dei desideri
Fattorizzazione dei numeri naturali. Evoluzione del metodo di Fermat e nuove scoperte
Disponibilità in 10 giorni lavorativi
11,88 €
-5%
12,50 €
11,88 €
12,50 €
-5%
Disp. in 10 gg
Altre offerte vendute e spedite dai nostri venditori
Libri
Fattorizzazione dei numeri naturali. Evoluzione del metodo di Fermat e nuove scoperte
Altri venditori
Prezzo e spese di spedizione
Nuovo
disponibilità in 10 giorni lavorativi
Venduto e spedito da
IBS
disponibilità in 10 giorni lavorativi
Spedizione Gratis
-5%
12,50 €
11,88 €
Spedizione 7,50 €
12,50 €
Altri venditori
Prezzo e spese di spedizione
Nuovo
disponibilità in 10 giorni lavorativi
Venduto e spedito da
IBS
disponibilità in 10 giorni lavorativi
Spedizione Gratis
-5%
12,50 €
11,88 €
Spedizione 7,50 €
12,50 €
Altri venditori
Prezzo e spese di spedizione
Tutti i formati ed edizioni
A partire dal crivello di Eratostene, sintesi del percorso storico della fattorizzazione dei numeri naturali con analisi dettagliata del metodo di Pierre de Fermat il quale ha individuato i divisori dei numeri composti ricavandoli da somma e differenza di radici di determinati quadrati perfetti. L'estensione del metodo di Fermat tramite apposite tabelle esplicative del fenomeno applicato a tutti i numeri dispari mette in rilievo caratteristiche divergenti fra numeri primi e numeri composti. Di seguito, un nuovo metodo di fattorizzazione scoperto dall'autore il quale, tramite apposite formule, da cicli continui di numeri naturali di forma 6k, 6k+1, 6k+2, 6k+3, 6k+4 e 6k-1, aventi ordinati divisori di valore crescente, consente di estinguere la possibilità che i numeri naturali di forma 6k±1 inseriti in tali scie, qualsiasi sia la loro dimensione, possano essere dei numeri primi.
Leggi di più
Leggi di meno
Tipo:
Libro universitario
Pagine:
56 p.
EAN:
9791221435436
L'articolo è stato aggiunto al carrello
Informazioni e Contatti sulla Sicurezza dei Prodotti
Le schede prodotto sono aggiornate in conformità al Regolamento UE 988/2023. Laddove ci fossero taluni dati non disponibili per ragioni indipendenti da IBS, vi informiamo che stiamo compiendo ogni ragionevole sforzo per inserirli. Vi invitiamo a controllare periodicamente il sito www.ibs.it per eventuali novità e aggiornamenti.
Per le vendite di prodotti da terze parti, ciascun venditore si assume la piena e diretta responsabilità per la commercializzazione del prodotto e per la sua conformità al Regolamento UE 988/2023, nonché alle normative nazionali ed europee vigenti.
Per informazioni sulla sicurezza dei prodotti, contattare productsafetyibs@feltrinelli.it
L’articolo è stato aggiunto alla lista dei desideri
